CS229：11-SVM（二）最优间隔分类器

最优间隔分类器（_Optimal Margin Classifier_）。其目标是使得最小几何间隔最大化（SVM（一）概念）：

$$\text{目标(1):} \\\ \max_{w, b} \gamma \\\ \text{ s.t. } y^{(i)} \cdot ((\frac{w}{||w||})^T \cdot x^{(i)}+\frac{b}{||w||}) \geq \gamma, i=1,\ldots,n$$

我们知道，$\hat{\gamma} = \frac{\gamma}{||w||}$，所以上面的目标可以等同于：

$$\text{目标(2):} \\\ \max_{w, b} \frac{\hat{\gamma}}{||w||} \\\ \text{ s.t. }y^{(i)} \cdot (w^T \cdot x^{(i)}+b) \geq \hat{\gamma}, i=1,\ldots,n$$

为了最大化上述值，我们有两种策略。

1. 增大$\hat{\gamma}$
2. 减小$||w||$

针对第一种可能，我们要证明其无效性。假如，我们增大$\hat{\gamma}$到${\hat{\gamma}}_1 := \lambda {\hat{\gamma}}$，因为$\hat{\gamma}=y(w^Tx+b)$，可以视作$w_1:=\lambda w, b_1 = \lambda b$。所以，此时

$$\frac{\hat{\gamma_1}}{||w_1||}=\frac{\lambda \hat{\gamma}}{||\lambda w||} = \frac{\hat{\gamma}}{||w||} \\\$$

没有发生任何改变，所以第一条策略不可行。于是，我们可以固定$\hat{\gamma}=1$

此时，上述目标(2)可以表述成：

$$\text{目标(3):} \\\ \min_{w, b} \frac{1}{2}||w||^2 \\\ \text{ s.t. }y^{(i)} \cdot (w^T \cdot x^{(i)}+b) \geq 1, i=1,\ldots,n$$

因为最小化$||w||$和最小化$\frac{1}{2}||w||^2$是一致的。

拉格朗日乘子法（Lagrange Multiplier）

为了解决上述的凸优化问题，我们引入拉格朗日乘子法Lagrange Multiplier来解决这个问题。

我们首先来看看凸优化问题的定义：

$$\min_wf(w) \\\ \text{s.t. }g_i(w) \leq 0, h_i(w) =0$$

构建拉格朗日乘子：

$${\cal L}(w, \alpha, \beta) = f(w)+\sum_i\alpha_ig_i(w)+\sum_i\beta_ih_i(w)$$

定义：

$$\theta_p(w) = \max_{\alpha_i>0, \beta}{\cal L}(w, \alpha, \beta)$$

观察$\theta_p(w)$：

1. 如果$g_i(w)>0$，那么$\theta_p(w)=+\infty$（因为$\alpha$可以取任意大值）。
2. 如果$h_i(w) \neq 0$，那么$\theta_p(w)=+\infty$（因为$\beta$可以取$+\infty/-\infty$）。

所以，在满足约束的情况下，$\theta_p(w)=f(w)$，$\min_w \theta_p(w)=\min_w f(w)$，因为使得${\cal L}(w, \alpha, \beta)$最大的方法，就是其他所有项全是 0。那么，可以得出这样的结论：

$$\theta_p(w)=\begin{cases} f(w), &\text{满足约束} \\\ \infty, &\text{不满足约束} \end{cases}$$

因此，在满足条件的情况下，$\min_w\theta_p(w)$等价于$min_wf(w)$。

我们将最优间隔分类器的目标重新表示一下：

$$p^\ast =\min_{w, b}\max_\alpha {\cal L(w, \alpha, b)} \\\ {\cal L}(w, \alpha, b) = \frac{1}{2}||w||^2+\sum_i\alpha_i(1-y^{(i)}(w^T x^{(i)}+b))$$

其中，直接忽略了$h_i(w)=0$的约束，而$g_i(w,b)=1-y^{(i)}(w^Tx^{(i)}+b) \leq 0, f(w)=\frac{1}{2}||w||^2$

对偶问题（Dual Problem）

一般来说，将原始问题转化成对偶问题来求解。一是因为对偶问题往往比较容易求解，二是因为对偶问题引入了核函数，方便推广到非线性分类的情况。

我们看到，之前的原始问题，是

$$p^\ast =\min_{w, b}\max_\alpha {\cal L}(w, \alpha, b)$$

那么，定义其对偶问题：

$$l^\ast =\max_\alpha\min_{w,b}{\cal L}(w, \alpha, b)$$

接下去，我们求解对偶问题：

先求解$\min_{w,b}{\cal L}(w, \alpha, b)$：

分别求偏导，使其等于 0，导出最小值：

$$\begin{align} & \nabla_w{\cal L}(w, \alpha, b) =w-\sum_{i=1}\alpha_iy^{(i)}x^{(i)}=0 \\\ & \nabla_b{\cal L}(w, \alpha, b) =\sum_{i=1}\alpha_iy^{(i)}=0 \end{align}$$

得到：

$$w =\sum_{i=1}\alpha_iy^{(i)}x^{(i)} \\\ \sum_{i=1}\alpha_iy^{(i)} = 0$$

代入${\cal L}(w, \alpha, b)$，就可以得到最小值：

$$\begin{align} {\cal L}(w, \alpha, b) &= \frac{1}{2}||w||^2+\sum_i\alpha_i(1-y^{(i)}(w^T x^{(i)}+b)) \\\ \min_{w, b}{\cal L}(w, \alpha, b) &=\underbrace{\sum_{i=1}\alpha_i-\frac{1}{2}\sum_{i=1}\sum_{j=1}\alpha_i\alpha_jy_iy_j(x_i \cdot x_j)}_{W(\alpha)} \end{align}$$

于是，我们的对偶问题简化到了对$W(\alpha)$最大化：

$$\max_\alpha W(\alpha) \\\ \text{s.t. }\alpha_i \geq 0, \sum_iy_i\alpha_i=0$$

假设，我们解得的对偶问题的解为：$\alpha^\ast =[\alpha_1^\ast ,\alpha_2^\ast , \ldots, \alpha_m^\ast ]$，那么最终原始问题的解可以表示成：

$$w^\ast =\sum_{i=1}\alpha_i^\ast y^{(i)}x^{(i)}$$

在原始问题中，还有$b$未得到解决。我们先来观察一下约束项：

$$g_i(w,b)=1-y{(i)}(w^Tx^{(i)}+b) \leq 0$$

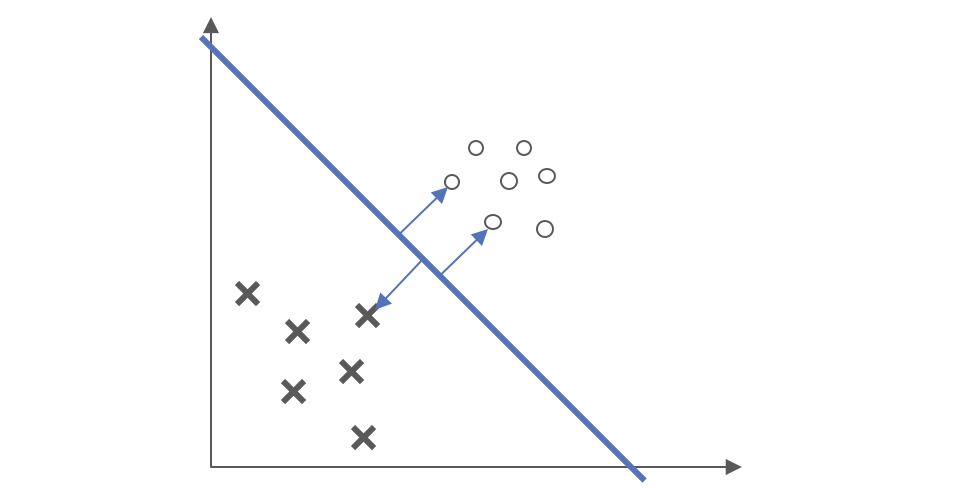
我们知道，在数据中，只有少数的几个数据点，他们的函数距离为 1（最小），也即$g_i(w,b)=0$，如图所示。

在整个数据集中，只有这些数据点对约束超平面起了作用，这些数据点被称为支持向量（_support vector_），其对应的$\alpha_i^\ast \neq 0$，而其他不是支持向量的数据点，没有对约束超平面起作用，其$\alpha_i^\ast =0$。

此时，我们已经得到了$w^\ast $，而$b^\ast $的计算如下，找到一个数据点，其$\alpha_j^\ast \neq 0$(也就是支持向量，其函数间隔为 1)，我们就能得到：

$$y^{(j)}(w^{*T}x^{(j)}+b^\ast )=1 \Rightarrow b^\ast =y^{(j)}-\sum_{i=1}\alpha_i^\ast y^{(i)}(x^{(i)} \cdot x^{(j)})$$